We have to find the equation of the line in standard form, knowing that the slope is m = -5 and it passes through the point (2, 1).
The standard form is:
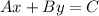
When we know the slope and one point, we can write the equation in slope-point form. Then, we can rearrange the terms in order to find the standard form.
The slope-point form is:
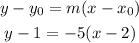
We then can rearrange it as:

Answer: the standard form of the line is 5x + y = 11.