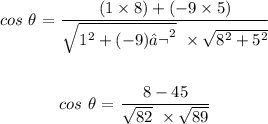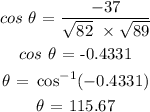Question

Find the angle between the vectors u = i – 9j and v = 8i + 5j.

Answer 1

`\theta\text{ = 115.67}\degree`

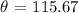
Step-by-step explanation:

Here, we want to find the angle between the two vectors

Mathematically, we have that as:

`cos\text{ }\theta\text{ = }(a.b)/(|a||b|)`

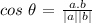
The denominator represents the magnitude of each of the given vectors as a product while the numerator represents the dot product of the two vectors

We have the calculation as follows:

`\begin{gathered} cos\text{ }\theta\text{ = }\frac{(1*8)+(-9*5)}{\sqrt{1^2+(-9)\placeholder{⬚}^2}\text{ }*√(8^2+5^2)} \\ \\ cos\text{ }\theta\text{ = }\frac{8-45}{√(82)\text{ }*√(89)} \\ \\ \end{gathered}`
`\begin{gathered} cos\text{ }\theta\text{ = }\frac{-37}{√(82)\text{ }*√(89)} \\ cos\text{ }\theta\text{ = -0.4331} \\ \theta\text{ = }\cos^(-1)(-0.4331) \\ \theta\text{ = 115.67}\degree \end{gathered}`