We have to write a quadratic equation, in factored form, that has an x-intercept at x=2 and x=-1, and a y-intercept 6.
As the x-intercepts are the roots of the function, we can write the equation as:
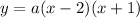
The parameter a will be defined in order to have a y-intercept at y=6. That means that, when x is 0, the value of the function is y=6.
Then, we can replace x with 0 and y with 6 and find the value of a:
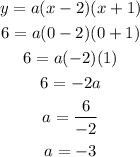
With the value of a=-3, we can write the factorized form of the equation as:
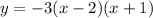
Graph:
Answer: y=-3(x-2)(x+1)