1 Answer

Bondt · Answer 1 · 2023-07-16T02:14:01+0000

Given

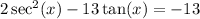
$2\sec ^2(x)-13\tan (x)=-13$

Add 13 to both sides

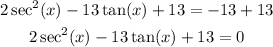
$\begin{gathered} 2\sec ^2(x)-13\tan (x)+13=-13+13 \\ 2\sec ^2(x)-13\tan (x)+13=0 \end{gathered}$

We have that

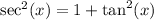
$\sec ^2(x)=1+\tan ^2(x)$

So, substitute in the above equation

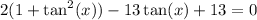
$2(1+\tan ^2(x))-13\tan (x)+13=0$

Simplify

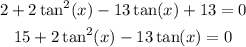
$\begin{gathered} 2+2\tan ^2(x)-13\tan (x)+13=0 \\ 15+2\tan ^2(x)-13\tan (x)=0 \end{gathered}$

Reordering the equation

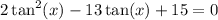
$2\tan ^2(x)-13\tan (x)+15=0$

We get a quadratic equation, then solve by factoring

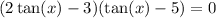
$(2\tan (x)-3)(\tan (x)-5)=0$

Separate the solutions

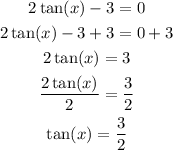
$\begin{gathered} 2\tan (x)-3=0 \\ 2\tan (x)-3+3=0+3 \\ 2\tan (x)=3 \\ (2\tan (x))/(2)=(3)/(2) \\ \tan (x)=(3)/(2) \end{gathered}$

And

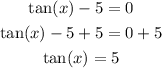
$\begin{gathered} \tan (x)-5=0 \\ \tan (x)-5+5=0+5 \\ \tan (x)=5 \end{gathered}$

Next, solve for x for each solution

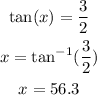
$\begin{gathered} \tan (x)=(3)/(2) \\ x=\tan ^(-1)((3)/(2)) \\ x=56.3 \end{gathered}$

And

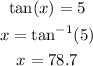
$\begin{gathered} \tan (x)=5 \\ x=\tan ^(-1)(5) \\ x=78.7 \end{gathered}$

Answer:

x = 56.3° and x = 78.7°

Please log in or register to add a comment.