The profit function can be gotten using the formula below:

where R(x) is the revenue function and C(x) is the cost function.
As previously calculated, the revenue and cost functions are given to be:
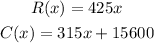
Therefore, the profit function is:
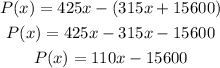
The profit to be made is $50,000. Equating the profit function to this amount, we can get the number of kayaks required. This is shown below:
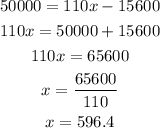
Therefore, the number of kayaks that must be sold is approximately 597 kayaks to make $50,000 in profits.