Question

According to psychologist IQs are normally distributed with a mean of 100 and a standard deviation of 19. What’s the percentage of the population has IQs above 154?

Answer 1

In order to solve this problem, we will calculate the z-score of the given data.

To do this, we use the formula,

`z=(x-\mu)/(\sigma)`

We plug in the given data:

`z=(154-100)/(19)\approx2.8421`

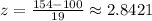
With this z-score, we can consult a z-score probability table or use an online resource. However, this will give us

`P(z<2.8421)`

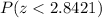
but we are interested in itbeing greater than it, so we must calculate

`1-P(z<2.8421)=1-0.99776=0.00224`

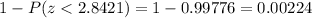
So, the percentage of the population that has an IQ above 154 is 0.224%.