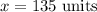Given: A right triangle is given, and an altitude is drawn to the hypotenuse of the triangle.
Required: To determine the missing side x.
Step-by-step explanation: The given triangle is as follows-
Let the side of the triangle be as shown in the figure. Now triangle ABD is a right-angled triangle. Hence, by Pythagoras theorem, we have-
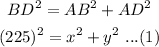
Similarly, triangles ABC and ADC are right-angled triangles. Thus-
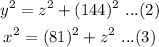
Equations (1), (2), and (3) represent equations in 3 variables. Hence solving equations (1) and (2) by substituting the value of y from equation (2) into equation (1) as follows-
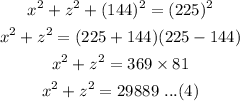
Now, we can solve equations (3) and (4) for x as follows-
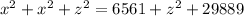
Further solving for x as-
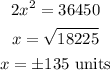
Since the side of a triangle can't be negative. Hence, x=135 units.
Final Answer: The length of the missing side is-