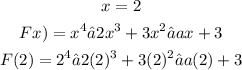Question

Use the Remainder Theorem to explain whether or not (x − 2) is a factor of F(x) = x4 − 2x3 + 3x2 − ax+ 3

Answer 1

Step-by-step explanation

The remainder theorem states that when a polynomial P(x) is divided by (x - a), for some number a, the remainder r is equal to P(a). Also states that when P(a) = 0, then (x - a) is a factor of P(x).

Then, let us see the result of evaluating the given polynomial when x = 2.

`\begin{gathered} x=2 \\ F\lparen x)=x^4−2x^3+3x^2−ax+3 \\ F(2)=2^4−2(2)^3+3(2)^2−a(2)+3 \end{gathered}`