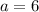Question

The position of an object is given by the formulasx = -3t² + 2t -4 and y = -2t³ + 6t² +1A) What is the speed at t = 1sB) What is the acceleration at t = 1s

Answer 1

We are given that the position of an object if given by the following equations:

`\begin{gathered} x=-3t^2+2t-4 \\ y=-2t^3+6t^2+1 \end{gathered}`

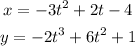
To determine the velocity we will determine the derivative of each of the functions. For "x" we have:

`x=-3t^2+2t-4`

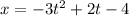
Finding the derivative with respect to time we get:

`(dx)/(dt)=(d)/(dt)(-3t^2+2t-4)`

Now we distribute the derivative on the left side:

`(dx)/(dt)=(d)/(dt)(-3t^2)+(d)/(dt)(2t)-(d)/(dt)(4)`

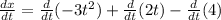
For the first derivative we will use the rule:

`(d)/(dt)(at^n)=ant^(n-1)`

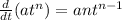
Applying the rule we get:

`(dx)/(dt)=-6t^{}+(d)/(dt)(2t)-(d)/(dt)(4)`

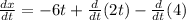
For the second derivative we use the rule:

`(d)/(dt)(at)=a`

Applying the rule we get:

`(dx)/(dt)=-6t^{}+2-(d)/(dt)(4)`

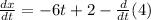
For the third derivative we use the rule:

`(d)/(dt)(a)=0`

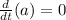
Applying the rule we get:

`(dx)/(dt)=-6t^{}+2`

Now, since the velocity is the derivative with respect to time of the position and this is and we determine the derivative for the x-position what we have found is the velocity in the x-direction, therefore, we can write:

`v_x=-6t^{}+2`

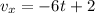
Now we substitute the value of time, t = 1, we get:

`\begin{gathered} v_x=-6(1)+2 \\ v_x=-6+2 \\ v_x=-4 \end{gathered}`

Now we use derivate the function for "y":

`(dy)/(dt)=(d)/(dt)(-2t^3+6t^2+1)`

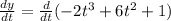
Using the same procedure as before we determine the derivative:

`(dy)/(dt)=-6t^2+12t`

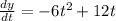
This is the velocity in the y-direction:

`v_y=-6t^2+12t`

Now we substitute the value of t = 1:

`\begin{gathered} v_y=-6(1)^2+12(1) \\ v_y=6 \end{gathered}`

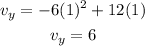
Now, the speed is the magnitude of the velocity, the magnitude is given by:

`v=\sqrt[]{v^2_x+v^2_y}`

Substituting the values we get:

`v=\sqrt[]{(-4)^2+6^2}`

Solving the operations:

`v=7.21`

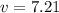
Therefore, the speed is 7.21 m/s.

To determine the acceleration we will determine the derivative of the formulas for velocities:

`v_x=-6t^{}+2`

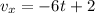
Now we derivate with respect to time:

`(dv_x)/(dt)=a_x=-6`

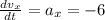
Now we use the function for the velocity in the y-direction:

`(dv_y)/(dt)=a_y=-12t^{}+12`

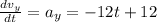
Now we substitute the value of t = 1:

`\begin{gathered} a_y=-12(1)^{}+12 \\ a_y=0 \end{gathered}`

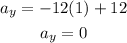
Since the acceleration in the y-direction is zero, this means that the total acceleration is the acceleration in the x-direction, therefore, the magnitude of the acceleration is:

`a=6`