Question

Directions: Drag each tile to the correct box.Put the recursive formulas below in order from least to greatest according to the value of their 10th terms.For all of the formulas, let n be equal to the whole numbers greater than or equal to one.

Answer 1

Solving for the 10th term for each of the recursive sequence

First sequence

`\begin{gathered} a_1=32 \\ a_(n+1)=-5+a_n \\ \\ \text{This can be converted to} \\ a_n=a_1+(n-1)(-5) \\ \\ \text{Substitute }n=10 \\ a_(10)=32+(10-1)(-5) \\ a_(10)=32+(9)(-5) \\ a_(10)=32-45 \\ a_(10)=-13 \end{gathered}`

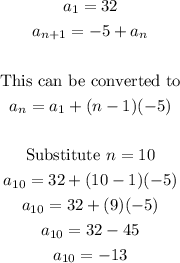
Second sequence

`\begin{gathered} a_1=2048 \\ a_(n+1)=-(1)/(2)a_n \\ \\ \text{This can be converted to} \\ a_n=a_1\cdot\Big(-(1)/(2)\Big)^(n-1) \\ \\ \text{Substitute }n=10 \\ a_(10)=2048\cdot\Big(-(1)/(2)\Big)^(10-1) \\ a_(10)=2048\cdot\Big(-(1)/(2)\Big)^9 \\ a_(10)=-4 \end{gathered}`

Third sequence

`\begin{gathered} a_1=0.125 \\ a_(n+1)=2a_n \\ \\ \text{This can be converted to} \\ a_n=a_1\cdot2^(n-1) \\ \\ \text{Substitute }n=10 \\ a_(10)=0.125\cdot2^(10-1) \\ a_(10)=0.125\cdot2^9 \\ a_(10)=64 \end{gathered}`

Fourth sequence

`\begin{gathered} a_1=-7(2)/(3) \\ a_(n+1)=a_n+1(2)/(3) \\ \\ \text{This can be converted to} \\ a_n=a_1+(n-1)\Big(1(2)/(3)\Big) \\ \\ \text{Substitute }n=10 \\ a_(10)=-7(2)/(3)+(10-1)\Big(1(2)/(3)\Big) \\ a_(10)=(-23)/(3)+(9)\Big((5)/(3)\Big) \\ a_(10)=-(23)/(3)+(45)/(3) \\ a_(10)=(22)/(3) \\ a_(10)=7(1)/(3) \end{gathered}`

Arranging the formulas from least to greatest according to their 10th terms, we have the following:

First Sequence → Second Sequence → Fourth Sequence → Third Sequence