the distance the ship travelled from point A to D is 582 ft
Step-by-step explanation:
To dtermine the distance from point A to D, we need to find the distance from point A to C and distance from point C to D
To get the distance from point C to D, we will consider triangle BCD:
opposite = 125 ft
DC = ?
angle = 16°
To get DC (adjacent), we will use tan ratio:
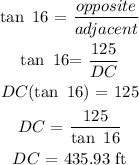
To get the distance from point A to C, we will consider triangle ABC:
opposite = 125 ft
AC = ?
angle = 7°
To get AC (adjacent), we will use tan ratio:

Distance AC = Distance DC + Distance AD
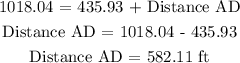
The distance the ship travelled from point A to D = Distance AD
To the nearest foot, the distance the ship travelled from point A to D is 582 ft