Question

Please walk me through these questions step by step (Simplifying the following terms)

Answer 1

The only formulas you have to know are:

`\begin{gathered} √(a\cdot b)=√(a)\cdot√(b) \\ i^2=-1\rightarrow i=√(-1) \end{gathered}`

When you do not know the root of a number, you have to express its root like a product of its main factors, for example:

`√(75)=5√(3)`

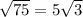
To find these factors, we can divide the original number among other numbers and multiply them, for example:

When we know those factors, we can use the laws of roots to simplify:

`\begin{gathered} 75=5^2\cdot3 \\ \sqrt[]{75}=√(5^2\cdot3)=5^{(2)/(2)}\cdot√(3)=5√(3) \end{gathered}`

With this in mind, we can now solve the exercise:

First term:

`\begin{gathered} (-20\pm√(75))/(5) \\ \\ (-20\pm5√(3))/(5)\text{ \lparen Divide each term of the numerator by the denominator\rparen} \\ \\ -4\pm\sqrt[]{3} \end{gathered}`

Second term:

*Notice that

`√(-81)=√((-1)\cdot(81))=√(81)\cdot√(-1)=√(81)i=9i`
`\begin{gathered} (6\pm√(-81))/(3) \\ \\ (6\pm9i)/(3) \\ \\ 2\pm3i \end{gathered}`

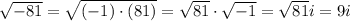
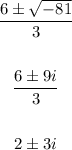
Third term:

*Notice the followings:

`√(-28)=√(28\cdot-1)=√(28)\cdot√(-1)=√(4\cdot7)i=2√(7)i`

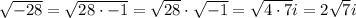
Finally,

`\begin{gathered} (-4\pm√(-28))/(8) \\ \\ (-4\pm2√(7)i)/(8) \\ \\ (-4)/(8)\pm(2√(7))/(8)i \\ \\ (-1)/(2)\pm(√(7))/(4)\imaginaryI \end{gathered}`