To solve this question, we would use cosine rule which is given as
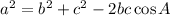
Our values have been defined for us and we will proceed to evaluate
![\begin{gathered} a^2=4^2+10^2-2(4)(10)\cos 41 \\ a^2=16+100-80\cos 41 \\ a^2=116-60.376 \\ a^2=55.624 \\ \text{take the square root of both sides} \\ a=\sqrt[]{55.624} \\ a=7.458\approx7.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/frd1btj3b4c3x8e2ortgjrcaztok86sfo2.png)
From the calculations above, the value of the missing side a is 7.5 units
To find angle B,
we can use sine rule
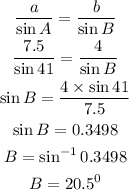
We can still approach C with sine rule or sum of angle in a triangle
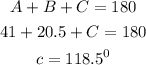
From the calculations above, the value of a = 7.5 , B = 22⁰ and C = 118.5⁰ respectively which is option B