Question

The organizer of a conference is selecting workshops to include. She will select from 5 workshops about genetics and 8 workshops about ethics. In how many ways can she select 6 workshops if fewer than 3 must be about genetics?

Answer 1

We have the following:

- 5 possible about genetics and need fewer than 3 (so it can be 0, 1 or 2).

- 8 about ethics

- want to select 6 in total.

We can calculate all the possible ways by doing it in three situations:

1 - From the 6, 0 will be genetics and 6 will be ethics

2 - From the 6, 1 will be genetics and 5 will be ethics

3 - From the 6, 2 will be genetics and 4 will be ethics

All of these will have to add up to find the total number of ways.

1 - 0 genetics, 6 ethics:

Since no genetics will be chosen, we can choose any 6 from the 8 possible about ethics, that is, we have a situation of "8 choose 6"

The equation for a situation "n choose k" and the number of ways in it is:

`n=(n!)/(k!(n-k)!)`

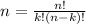
So, if we have "8 choose 6":

`n_1=(8!)/(6!(8-6)!)=(8\cdot7\cdot6!)/(6!2!)=(8\cdot7)/(2)=4\cdot7=28`

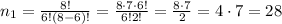
So, in this first we have 28 ways.

2 - 1 genetics, 5 ethics:

Here, we will have one equation for each and the total number of ways will be the multiplication of both.

For genetics, we have to pick 1 from 5, so "5 choose 1":

`(5!)/(1!(5-1)!)=(5\cdot4!)/(4!)=5_{}`

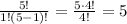
For ethics, we have to pick 5 from 8, so "8 choose 5":

`(8!)/(5!(8-5)!)=(8\cdot7\cdot6\cdot5!)/(5!3!)=(8\cdot7\cdot6)/(3\cdot2)=8\cdot7=56`

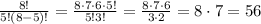
So, the total number of ways is the multiplicatinos of them:

`n_2=5\cdot56=280`

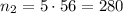
3 - 2 genetics, 4 ethics:

Similar to the last one.

For genetics, we have to pick 2 from 5, so "5 choose 2":

`(5!)/(2!(5-2)!)=(5\cdot4\cdot3!)/(2\cdot3!)=\frac{5_{}\cdot4}{2}=5\cdot2=10`

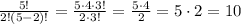
For ethics, we have to pick 4 from 8, so "8 choose 4":

`(8!)/(4!(8-4)!)=(8\cdot7\cdot6\cdot5\cdot4!)/(4!4!)=(8\cdot7\cdot6\cdot5)/(4\cdot3\cdot2)=2\cdot7\cdot5=70`

So, the total number of ways is the multiplicatinos of them:

`n_3=10\cdot70=700`

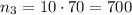
Now, the total number of ways is the sum of all these possibilities, so:

`\begin{gathered} n=n_1+n_2+n_3 \\ n=28+280+700 \\ n=1008 \end{gathered}`

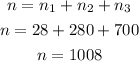
So, the total number of ways is 1008.