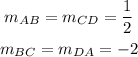Question

Make use of structure. For rectangle ABCD, two vertices are A(-2, 3) and B(4, 6). Find the slopes of BC, CD, and DA. Explain your answer.

Answer 1

We are given a rectangle ABCD

A(-2, 3)

B(4, 6)

We are asked to find the slopes of sides BC, CD, and DA.

Let me first draw a rectangle to better understand the problem

Recall that the slope is given by

`m=(y_2−y_1)/( x_2−x_1)`
`\text{where}(x_1,y_1)=(-2,3)\text{and}(x_2,y_2)=(4,6)`

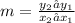
So the slope of side AB is

`m_(AB)=(6-3)/(4-(-2))=(3)/(4+2)=(3)/(6)=(1)/(2)=0.5`

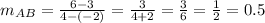
The sides BC and DA are perpenducluar to the side AB.

So their slopes will be

`m_(BC)=m_(DA)=(1)/(-m_(AB))`

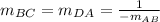
Substituting the value of slope of AB

`m_(BC)=m_(DA)=(1)/(-0.5)=-2`

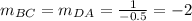
The side CD is parallel to the side AB.

Parallel sides have equal slopes so

`m_(CD)=m_(AB)=(1)/(2)`

Therefore, the slopes of the rectangle ABCD are

`\begin{gathered} m_(AB)=m_(CD)=(1)/(2) \\ m_(BC)=m_(DA)=-2 \end{gathered}`