We need to find the vertex of the parabola
Vertex (h,k) is given by the following formula:
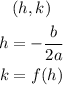
Where, a and b are coefficients of the quadratic equation

in this example:
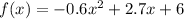
Therefore,
a = 0.6
b = 2.7
Now, we know that, we can find vertex (h,k)
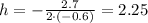
now, let's determine k
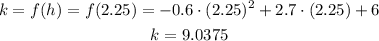
So, the vertex of the parabola is the point (2.25 , 9.0375)
This means that the maximum height of the ball is k = 9.0375 ft and it occurs h = 2.25 ft from where it was thrown