We know that the probability in a normal distribution can be obtained by the z score, the z score is given as:
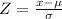
where mu is the mean and sigma is the standard deviation. In this case we have:
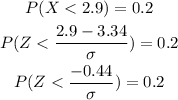
Now, to have 20% (that is 0.2) we need that the z score to be -0.842, then we have:
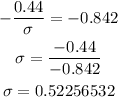
Therefore the standard deviation is $0.52