The demand equation is given to be:
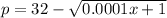
where p is the price and x is the number of units sold.
If the price per unit is $14.75, the number of units will be calculated as follows:
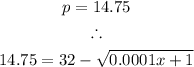
Subtracting 32 from both sides, we have:
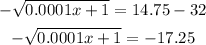
Multiply both sides by -1:
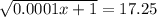
Square both sides:
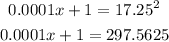
Subtract 1 from both sides:
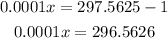
Divide both sides by 0.0001:
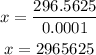
The number of units sold will be 2,965,625 units.