Question

A regular polygon with 9 sides (a nonagon) has a perimeter of 72 inches. What is the area of this polygon? Provide mathematical evidence.

Answer 1

The perimeter of the regular nonagon is 72 inches, the length of each side can be determined as,

`\begin{gathered} P=9s \\ 72=9s \\ s=8\text{ inches} \end{gathered}`

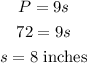
The diagram can be drawn as,

The value of apopthem a can be determined as, where n is the number of sides,

`\begin{gathered} a=(s)/(2\tan ((180^(\circ))/(n))) \\ =(8)/(2\tan20^(\circ)) \\ =10.98\text{ in} \end{gathered}`

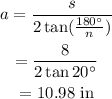
The area can be determined as,

`\begin{gathered} A=(P* a)/(2) \\ =\frac{72\text{ inches}*10.98\text{ inches}}{2} \\ =395.63in^2 \end{gathered}`

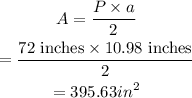
Thus, the required area of the polygon is 395.63 square inches.