1.
First, let's calculate the volume of the cube:
![V_1=6^3=216\text{ cm^^b3}]()
Now, let's calculate the volume of the cylinder drilled:
![\begin{gathered} V_2=(\pi d^2h)/(4)\\ \\ V_2=(3.14159\cdot2.5^2\cdot6)/(4)\\ \\ V_2=29.45\text{ cm^^b3} \end{gathered}]()
So the volume of the cube after being drilled is:
![\begin{gathered} V=V_1-V_2\\ \\ V=216-29.45\\ \\ V=186.55\text{ cm^^b3} \end{gathered}]()
If the weight is 6.3 N, let's find the mass:
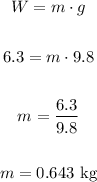
And the density of the metal is:
![\begin{gathered} d=(m)/(V)\\ \\ d=(0.643)/(186.55)\\ \\ d=0.0034468\text{ kg/cm^^b3}\\ \\ d=3.4468\text{ g/cm^^b3} \end{gathered}]()
2.
To find the weight of the cube before being drilled, let's use the following rule of three:
![\begin{gathered} volume\rightarrow weight\\ \\ 216\text{ cm^^b3}\rightarrow x\text{ N}\\ \\ 186.55\text{ cm^^b3}\rightarrow6.3\text{ N}\\ \\ \\ \\ (216)/(186.55)=(x)/(6.3)\\ \\ x=(216\cdot6.3)/(186.55)\\ \\ x=7.295\text{ N} \end{gathered}]()