Question

I’m not sure on how to do it right as I keep getting this wrong. Please help!

Answer 1

Given the function:

`A(t)=40(0.83)^t`

Where A(t) shows the amount of drug in a body after t hours.

Let's solve for the following:

• (a). Initial dosage:

Apply the exponential functions:

`f(x)=a(b)^x`

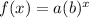
Where:

a is the initial value

b is the change factor.

Thus, we have the following:

a = 40

b = 0.83

Therefore, the initial dose is 40 mg.

• (b). What percent leaves the body each hour?

Apply the function:

`f(x)=a(1-r)^x`

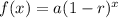
Where:

r is the decay rate.

Thus, we have:

b = 1 - r

r = 1 - b

r = 1 - 0.83

r = 0.17

The percent that leaves the body each hour will be:

0.17 x 100 = 17%

Therefore, 17 percent of the drug leaves the body each hour.

• (c). What amount of drug is left after 12 hours?

Substitute 12 for t and solve for A(12):

`\begin{gathered} A(12)=40(0.83)^(12) \\ \\ A(12)=40(0.1068900077) \\ \\ A(12)=4.28 \end{gathered}`

The amount left after 12 hours is 4.28 mg.

• (d). The first whole number of hours at which there is less than 6 mg left.

Plug in 5.9 for A(t) and solve for t.

`5.9=40(0.83)^t`

Divide both sides by 40:

`\begin{gathered} (5.9)/(40)=(40(0.83)^t)/(40) \\ \\ 0.1475=(0.83)^t \end{gathered}`

Take the natural logarithm of both sides:

`\begin{gathered} ln(0.1475)=tln(0.83) \\ \\ t=(ln(0.1475))/(ln(0.83)) \\ \\ t=10.2 \end{gathered}`

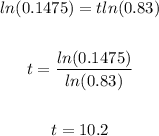
Therefore, the first whole number of hours where there is less than 6 mg left is 10 hours.

ANSWER:

• (a) 40 mg

,

• (b) 17%

,

• (c). 4.28 mg

,

• (d). 10 hours