Given:
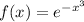
To find the vertical and horizontal asymptotes:
The line x=L is a vertical asymptote of the function f(x) if the limit of the function at this point is infinite.
But, here there is no such point.
Thus, the function f(x) doesn't have a vertical asymptote.
The line y=L is a vertical asymptote of the function f(x) if the limit of the function (either left or right side) at this point is finite.

Thus, y = 0 is the horizontal asymptote for the given function.