Question

Out of 167 randomly selected adults in the United States who were surveyed, 70 exercise on a regular basis. Construct a 90% confidence interval for the proportion of all adults in the United States who exercise on a regular basis. Round to three decimal places

Answer 1

(0.356, 0.482)

Explanation:

The first thing is to calculate the proportion with the data of the statement:

`\begin{gathered} p=(x)/(n)=(70)/(167) \\ \\ p=0.4192 \end{gathered}`

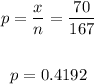
For a 90% confidence interval, we have that the value of Z is the following:

`\begin{gathered} \alpha=1-90\% \\ \\ \alpha=1-0.9=0.1 \\ \\ \alpha\text{/2}=(0.1)/(2)=0.05 \\ \text{ } \\ \text{The corresponding value of Z would be:} \\ \\ Z_{\alpha\text{/2}}=1.645 \end{gathered}`

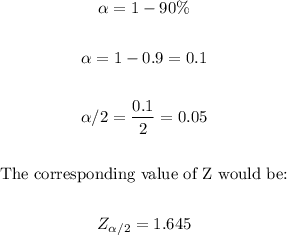
We calculate the interval as follows:

`\begin{gathered} \text{ Upper limit }=p+Z_{\alpha\text{/2}}\cdot\sqrt{(p\cdot(1-p))/(n)}=0.4192+1.645\cdot\sqrt{(0.4192\cdot\left(1-0.4192\right))/(167)}\:=0.482 \\ \\ \text{ Lower limit}=p-Z_{\alpha\text{/2}}\cdot\sqrt{(p\cdot(1-p))/(n)}=0.4192-1.645\cdot\sqrt{(0.4192\cdot\left(1-0.4192\right))/(167)}\:=0.356 \end{gathered}`

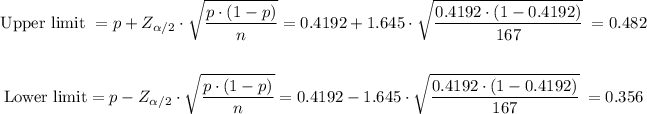
The 90% confidence interval for the proportion of all adults in the United States is (0.356, 0.482)