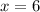Question

The rest of the question say what is the length of the tangent line labeled X

Answer 1

To solve this problem, consider the following picture

By the tangent secant segment theorem we have the following equation

`a^2=b\cdot(b+c)`

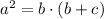
Note that in our case, we have a=x, b=3 and c=9. So if we replace this values in the equation, we have

`x^2=3\cdot(3+9)=3\cdot12=36`

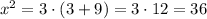
so, applying the square root on both sides, we get

`x=\sqrt[]{36}=\pm6`

Since x is a distance, it should be strictly positive, so we have that

`x=6`