ANSWER
All real numbers
Step-by-step explanation
To solve this inequality, first, divide both sides by 3,
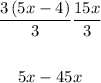
Then, subtract 5x from both sides of the inequality,
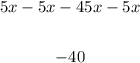
-4 indeed is less than 0, and this is valid for any value of x in the real numbers - i.e. any real number for x satisfies the inequality.
Hence, the solution is all real numbers.