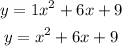The general form of a quadratic is:

We need to plug in the 3 pair of points into "x" and "y" and simultaneously solve the 3 equations for a, b, and c.
Putting (0,9):
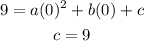
Putting (-6,9):
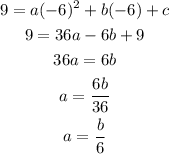
Putting (-5,4):
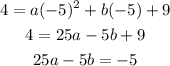
We substitute a=b/6 into this equation and solve for b:

Thus, "a" will be:
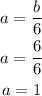
Thus, we have a = 1, b = 6, c = 9
The equation is: