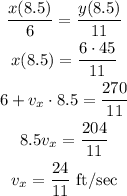Question

A street light is at the top of a 17ft tall pole. A woman 6ft tall walks away from the pole with a speed of 4ft/sec along a straight path. How fast is the tip of her shadow moving when she is 45ft from the base of the pole?

Answer 1

A woman 6 ft tall walks away from a 17 ft tall pole with a street light on top of it.

Graphically:

From the diagram, we can say that:

`(x)/(6)=(y)/(11)\ldots(1)`

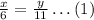
The laws of motion of the woman and the shadow with respect to the base of the pole are:

`\begin{gathered} y(t)=y_0+v_y\cdot t \\ x(t)=x_0+v_x\cdot t \end{gathered}`

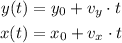
Where x0 and y0 are the initial positions, vx and vy are the shadow speed and the speed of the woman, respectively. We know that vy = 4 ft/s, so if we say that the starting point for the woman was 11 feet away from the pole, then using equation (1):

`\begin{gathered} y_0=11 \\ (x_0)/(6)=(y_0)/(11)\Rightarrow x_0=6 \end{gathered}`

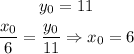
Then, the laws of motion are:

`\begin{gathered} y(t)=11+4\cdot t \\ x(t)=6+v_x\cdot t \end{gathered}`

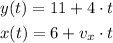
We now calculate the instant of time when y = 45 ft. Using the law of motion of the woman:

`\begin{gathered} 45=11+4\cdot t \\ 34=4\cdot t \\ t=8.5\text{ sec} \end{gathered}`

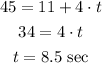
Again, using the equation (1):

`\begin{gathered} (x(8.5))/(6)=(y(8.5))/(11) \\ x(8.5)=(6\cdot45)/(11) \\ 6+v_x\cdot8.5=(270)/(11) \\ 8.5v_x=(204)/(11) \\ v_x=(24)/(11)\text{ ft/sec} \end{gathered}`