ANSWER
0.0001984
Step-by-step explanation
There are 10 possible values for each digit of the passcode to enter the building.
These include: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
So, there are:10 x 10 x 10 x 10 = 10^4 = 10,000 total possible passcodes.
For no repeat passcode
We have: 10 x 9x 8 x7 = 5040 total possible passcodes without repetition.
Probability of guessing correct sequence
Since there is only 1 correct sequence of 4 digits passcode (without repetition) to enter the building
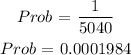
Hence, the probability that they guess the correct sequence is 0.0001984