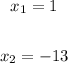Given the quadratic equation:
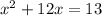
We can rewrite the equation as follows:
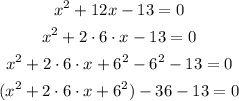
We see that the term inside the parenthesis is a perfect square polynomial. Then:
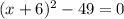
Solving for x:
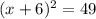
Taking the square on both sides:
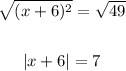
This equation can turn into two equations:
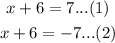
Solving (1):
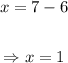
Solving (2):
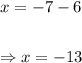
Finally, the solutions to the equation are: