Explanation:
We are given information about the height of a flagpole and its shadow, and we also have information about the shadow of a hill.
This information is represented in the following diagram:
Where the symbol '?' represents what we are trying to find:
How tall is the hill
We will call this h for reference:
Since these shadows are happening at the same time, the ratio between these values must be the same, this is to say that
3/5 must be equal to h/62:
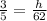
From this equation, we solve to find h:
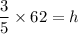
Solving the operations the result is:
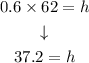
The hill is 37.2 m tall.
Answer:
37.2 m