Question

(a) Find an angle between 0 and 2pi that is coterminal with 10pi/3.(b) Find an angle between 0° and 360° that is coterminal with -300°.Give exact values for your answers.(a) __ radians(b) __ °

Answer 1

To find a coterminal angle between 0 and 2pi, you can subtract 2pi from the given angle, like this

`(10\pi)/(3)-2\pi\text{ }`

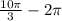
To do the subtraction, you can convert 2pi into a fraction, like this

`(2\pi\cdot3)/(3)=(6\pi)/(3)`

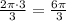
So, you have

`(10\pi)/(3)-2\pi=(10\pi)/(3)-(6\pi)/(3)=(4\pi)/(3)`

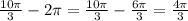
Therefore, 4pi/3 is the angle between 0 and 2pi that y is coterminal with 10pi/3.

For point (b), you can add 360° at the angle given, like this

`360+(-300)=360-300=60`

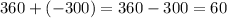
Therefore, an angle between 0° and 360° that is coterminal with -300° is 60°.