Question

A phonograph record has an initial angular speed of 33 rev/min . The record slows to 11 rev/min in 2.0 seconds. What is the records angular acceleration in rad/s2 during this time interval ?

Answer 1

In order to calculate the angular acceleration, we can use the following formula:

`a=(v_f-v_i)/(t)`

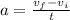
Where vf is the final angular speed, vi is the initial angular speed and t is the interval of time.

Since the speed is in rev/min, we need to convert to rad/s.

Knowing that 1 rev = 2π rad and 1 min = 60 s, we have:

`\begin{gathered} 33\text{ rev/min}=33\cdot\frac{2\pi\text{ rad}}{60\text{ s}}=3.456\text{ rad/s} \\ 11\text{ rev/min}=11\cdot\frac{2\pi\text{ rad}}{60\text{ s}}=1.152\text{ rad/s} \end{gathered}`

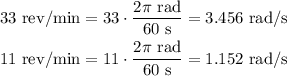
Now, using vf = 1.152, vi = 3.456 and t = 2, we have:

`a=(1.152-3.456)/(2)=(-2.304)/(2)=-1.152\text{ rad/s2}`

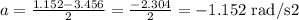
So the angular acceleration is -1.152 rad/s².