Question

Part 1: Person A has a car with the average fuel consumption of 20 miles per gallon. Person B has an average fuel consumption of 30 miles per gallon. Person C has an average fuel consumption of 40 miles per gallon. they are trying to work out how much fuel they will each save if they change cars. Person A, " I am going to buy Person B's car." Person B says, " I am going to buy Person C's car." Person C says that each week they will both save the same amount of fuel.Is person C correct? Part 2: Person C wants to buy a new car. Each week, he wants to save the same amount of fuel as person A saved. What average fuel consumption should person C look for in a new car?

Answer 1

Let's assum that each person drives 120 miles per week.

Then for person A we have:

`\begin{gathered} 20mi\rightarrow1\text{gal} \\ 120mi\rightarrow xgal \\ \Rightarrow x=(120)/(20)=6gal \\ x=6\text{gal} \end{gathered}`

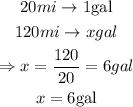
for person B we have:

`\begin{gathered} 30mi\rightarrow1gal \\ 120mi\rightarrow xgal \\ \Rightarrow x=(120)/(30)=4gal \\ x=4\text{gal} \end{gathered}`

finally, for person C:

`\begin{gathered} 40mi\rightarrow1gal \\ 120mi\rightarrow xgal \\ \Rightarrow x=(120)/(40)=3gal \\ x=3\text{gal} \end{gathered}`

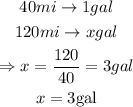
Then, if person A changes to person B's car, we have that the save is:

`6-4=2`

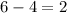
if person B buys person C's car, then the save is:

`4-3=1`

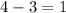
therefore, the savings on gas will be different for both of them and person C is incorrect.

2)Since person A saved 2 gallons, then the new car for Person C must save 2 gallons for each mile traveled.

Then we have the following equation:

`3-x=2`

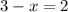
where 'x' represents the number of gallons consumed in 120 miles. then, solving for x we have:

`\begin{gathered} 3-x=2 \\ \Rightarrow-x=2-3=-1 \\ \Rightarrow-x=-1 \\ x=1 \end{gathered}`

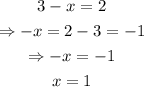
therefore, person C will need to buy a car that uses 1 gallon for eah 120 miles traveled