Question

Find the area between the graph of y= -12x^3 and the x-axis on the interval [-1, 1]. Write the exact answer. Do not round.

Answer 1

Recall that the integral of the area between the graph of two functions, in an interval [a,b] is:

`\int ^b_a|f(x)-h(x)|dx\text{.}`

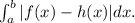
Now, if f(x) is an odd function, we can use the following property:

`\int ^a_(-a)|f(x)|dx=2\int ^a_0|f(x)|dx\text{.}`

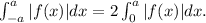
Now, notice that the function y=-12x³ is an odd function, therefore:

`\int ^1_(-1)|y-0|dx=2\int ^1_0|-12x^3|dx=2\int ^1_012x^3dx\text{.}`

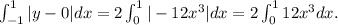
Applying the linearity of the integral we get:

`24\int ^1_0x^3dx=24(x^4)/(4)|^1_0=24((1)/(4)-0)=(24)/(4)=6.`

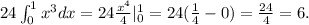
Answer: 6.