Question

Two skydivers jump from an airplane at an altitude of 5000m. Suppose one is 57 kg and the other is 68 kg. Using the data given in the example in class to find the amount of time each takes to get to the ground.Area = 0.18 m² air density = 1.21 kg/m³ drag coefficient C = .070

Answer 1

Given:

Two skydivers jump from an airplane at an altitude of: d = 5000 m

The mass of the first skydiver is: m1 = 57 kg

The mass of the second skydiver is: m2 = 68 kg

Area = 0.18 m²

Air density = 1.21 kg/m³

Drag Coefficient: C = 0.070

To find:

The amount of time each skydiver takes to get to the ground.

Step-by-step explanation:

The magnitude of drag force which acts opposite in the opposite direction is equal to the weight of the skydiver. Thus, the magnitude of the drag force can be calculated as:

`\begin{gathered} F_1=m_1g=57\text{ kg}*9.8\text{ m/s}^2=558.6\text{ kg.m/s}^2 \\ \\ F_2=m_2g=68\text{ kg}*9.8\text{ m/s}^2=666.4\text{ kg.m/s}^2 \end{gathered}`

Here, F1 is the magnitude of the drag force on the first skydiver and F2 is the drag force on the second skydiver.

The expression for drag force relating to the velocity is given as:

`F=(1)/(2)C\rho Av^2`

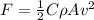
For the first skydiver the drag force is given as:

`\begin{gathered} F_1=(1)/(2)C\rho Av_1^2 \\ \\ \text{ Substituting the values in the above equation, we get:} \\ \\ 558.6\text{ kg.m/s}^2=(1)/(2)*0.070*1.21\text{ kg/m}^3*0.18\text{ m}^2* v_1^2 \\ \\ 558.6\text{ kg.m/s}^2=7.623*10^(-3)\text{ kg/m}* v_1^2 \\ \\ v_1^2=\frac{558.6\text{ kg.m/s}^2}{7.623*10^(-3)\text{ kg/m}} \\ \\ v_1^2=73278.24\text{ m}^2\text{/s}^2 \\ \\ v_1=\sqrt{73278.24\text{ m}^2\text{/s}^2} \\ \\ v_1=270.70\text{ m/s} \end{gathered}`

The velocity v1 of the first skydiver is 270.70 m/s.

The time t1 taken by the first skydiver to get to the ground can be calculated as:

`\begin{gathered} v_1=(d)/(t_1) \\ \\ t_1=(d)/(v_1) \\ \\ \text{ Substituting the values in the above equation, we get:} \\ \\ t_1=\frac{5000\text{ m}}{270.70\text{ m/s}} \\ \\ t_1=18.47\text{ s} \end{gathered}`

The first skydiver takes 18.47 seconds to get to the ground.

For the second skydiver, the drag force is given as:

`\begin{gathered} F_2=(1)/(2)C\rho Av_2^2 \\ \\ \text{ Substituting the values in the above equation, we get:} \\ \\ 666.4\text{ kg.m/s}^2=(1)/(2)*0.070*1.21\text{ kg/m}^3*0.18\text{ m}^2* v_2^2 \\ \\ 666.4\text{ kg.m/s}^2=7.623*10^(-3)\text{ kg/m}* v_2^2 \\ \\ v_2^2_{{}}=\frac{666.4\text{ kg.m/s}^2}{7.623*10^(-3)\text{ kg/m}} \\ \\ v_2^2=87419.65\text{ m}^2\text{/s}^2 \\ \\ v_2=\sqrt{87419.65\text{ m}^2\text{/s}^2} \\ \\ v_2=295.67\text{ m/s} \end{gathered}`

The velocity v2 of the second skydiver is 259.67 m/s.

The time t2 taken by the second skydiver to get to the ground can be calculated as:

`\begin{gathered} v_2=(d)/(t_2) \\ \\ t_2=(d)/(v_2) \\ \\ \text{ Substituting the values in the above equation, we get:} \\ \\ t_2=\frac{5000\text{ m}}{295.67\text{ m/s}} \\ \\ t_2=16.91\text{ s} \end{gathered}`

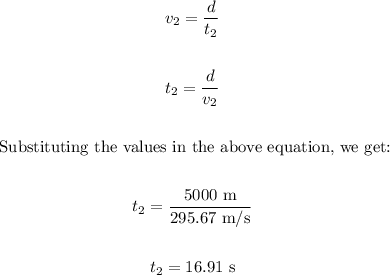
The second skydiver takes 16.91 seconds to get to the ground.

Final answer:

The first skydiver takes 18.47 seconds to get to the ground.

The second skydiver takes 16.91 seconds to get to the ground.