We have to find the expression for the composition
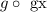
Where
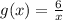
And express its domain in set notation. We will start by finding the expression for the composition
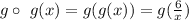
that is we firsts evaluate the inner functions that in this case is g, now taking as argument y=6/x, we evaluate the outer function that in this case also is g, as follows:
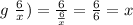
That is, the composition g*g is equal to x, the identity.
Now we will find the domain of g*g:
Note that the domain of a composition is an interception, as follows:
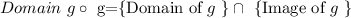
Therefore, we have to find the domain and image of g, and intercept both sets. We start with the domain of g_
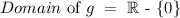
That is all the real numbers except the 0. Now note that the image of g is
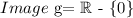
Finally, the domain of the composition g*g, can be obtained by the formula above:
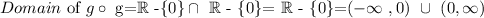
Therefore, the domain of the composition are all the real numbers excluding the 0.
-