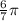Question

hello can yoy help with this plane trigonometry question and in the question turn it into radians and thank you for your time for helping me

Answer 1

The angle between 0 and 2 pie that is coterminal to the given angle is;

`(6)/(7)\pi`

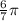
Step-by-step explanation:

We want to find the angle between 0 and 2 pie that is coterminal to;

`(34)/(7)\pi`

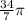
Angles that are coterminal with the given angle can be calculated using the formula;

`x+n2\pi=(34)/(7)\pi`

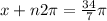
Where n=1,2,3...

and x is the coterminal angle.

At n = 1;

`\begin{gathered} x+2\pi=(34)/(7)\pi \\ x=(34)/(7)\pi-2\pi \\ x=(34)/(7)\pi-(14)/(7)\pi \\ x=(20)/(7)\pi \end{gathered}`

at n=2;

`\begin{gathered} x+2(2\pi)=(34)/(7)\pi \\ x+4\pi=(34)/(7)\pi \\ x=(34)/(7)\pi-4\pi \\ x=(34)/(7)\pi-(28)/(7)\pi \\ x=(6)/(7)\pi \end{gathered}`

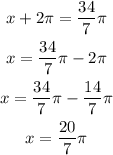
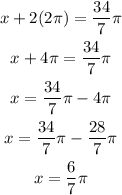
At n=2;

The value of x is between 0 and 2pie;

So, the angle between 0 and 2 pie that is coterminal to the given angle is;

`(6)/(7)\pi`