If the triangles MNQ and MOP are similar, then you know that the corresponding sides are at the same ratio. Because of this property, we can determine that:
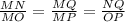
We know the measure of the corresponding sides MQ=12cm and MO=24cm, and the measure of the corresponding side to NQ, using these measures we can calculate NQ as follows:
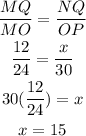
Side NQ measures 15 cm
The correct option is B.