Question

How many ways can a person toss a coin 14 times so that the number of heads is between 6 and 9 inclusive?

Answer 1

How many ways can a person toss a coin 14 times so that the number of heads is between 6 and 9 inclusive?​

the formula of combination is equal to

`\text{nCr}=(n!)/(r!(n-r)!)`

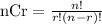
For r between 6 and 9

For r=6

n=14

substitute

`14\text{C6}=(14!)/(6!(14-6)!)=(14!)/(6!(8)!)=(14\cdot13\cdot12\cdot11\cdot10\cdot9)/(6\cdot5\cdot4\cdot3\cdot2\cdot1)`

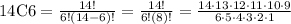
14C6=3,003

For r=7

n=14

substitute

`14\text{C7}=(14!)/(7!(14-7)!)=(14!)/(7!(7)!)=(14\cdot13\cdot12\cdot11\cdot10\cdot9\cdot8)/(7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)`

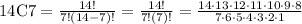
14C7=3,432

For r=8

n=14

substitute

`14\text{C8}=(14!)/(8!(14-8)!)=(14!)/(8!(6)!)=(14\cdot13\cdot12\cdot11\cdot10\cdot9)/(6\cdot5\cdot4\cdot3\cdot2\cdot1)`

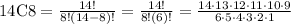
14C8=3,003

For r=9

n=14

substitute

`14\text{C9}=(14!)/(9!(14-9)!)=(14!)/(9!(5)!)=(14\cdot13\cdot12\cdot11\cdot10)/(5\cdot4\cdot3\cdot2\cdot1)`

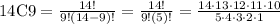
14C9=2,002

adds the combinations

3,003+3,432+3,003+2,002=11,440

11,440 ways