To solve the exercise, you can first draw a picture to better understand the statement. So,
Now, in a rectangle, the lengths of the diagonals measure the same. So,
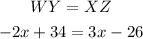
To solve for x first subtract 34 from both sides of the equation
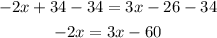
Subtract 3x from both sides of the equation
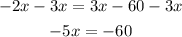
Divide by -5 into both sides of the equation
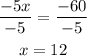
Finally, replace the value of x in the length of any of the diagonals, for example, the diagonal WY
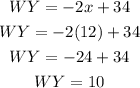
Therefore, the length of each diagonal is 10 units.