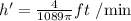
STEP - BY - STEP EXPLANATION
What to find?
dh/dt
Given that;
At a sand and gravel plant, sand is falling off a conveyor and onto a conical pile at a rate of 4 cubic feet per minute. The diameter of the base of the cone is approximately three times the altitude.
Since we have that the rate is 4 cubic per minute, then dv/dt = 4 (since v is the volume of the cone at time t.)
The formula for the volume of a cone is

Where r is the radius and h is the height.
We have that, the diameter of the cone is approximately three times the altitude.
That is;
diameter = 3h
But, d = 2r
⇒2r = 3h
⇒ r = 3h/2
Now, we substitute r=3h/2 into equation (1).
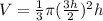
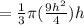
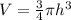
Now, differentiate the above with respect to t.
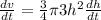
Simplify .
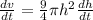
Make dh/dt subject of formula.

Recall that, dv/dt = 4 and h=22
Substituting the values into equation (2), we have;
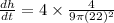
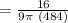
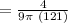
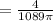
Therefore, h' = dh/dt = 4/1089π ft/min.