Question

Go5. Given functions f(x) = 9x – 2, g(x) = 5 – 3x/2, and h(x) = 4x – 7/4(a) Find g(-8).(b) Find the value of x that makes g(x) = -7.(c) Find the value of x that makes f(x) = g(x).(d) Find the value of x that makes f(x) = h(x)(e) Find the x-intercept of h(x).

Answer 1

a) g(-8) = 17

b) When g(x) = -7, x = 8

c) When f(x) = g(x), x = (2/3)

d) When f(x) = h(x), x = (1/20)

e) x-intercept of h(x) = (7/16)

Step-by-step explanation

f(x) = 9x - 2

g(x) = 5 - 3x/2

h(x) = 4x - 7/4

(a) Find g(-8).

g(x) = 5 - 3x/2

g(-8) means the value of g(x) when x = -8

g(-8) = 5 - [3×-8/2]

= 5 - (-12)

= 5 + 12

= 17

(b) Find the value of x that makes g(x) = -7.

g(x) = 5 - 3x/2

When g(x) = -7,

5 - 3x/2 = -7

5 - (3x/2) - 5 = -7 - 5

-(3x/2) = -12

`\begin{gathered} (-3x)/(2)=-12 \\ \text{Cross multiply} \\ -3x\text{ = 2}*-12 \\ -3x\text{ = -24} \\ \text{divide both sides by -3} \\ (-3x)/(-3)=(-24)/(-3) \\ x\text{ = 8} \end{gathered}`

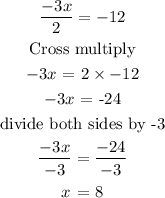
(c) Find the value of x that makes f(x) = g(x).

f(x) = 9x - 2

g(x) = 5 - 3x/2

When f(x) = g(x)

9x - 2 = 5 - (3x/2)

9x + (3x/2) = 5 + 2

(21x/2) = 7

`\begin{gathered} (21x)/(2)=7 \\ \text{Cross multiply} \\ 21x\text{ = 2}*7 \\ 21x=14 \\ \text{Divide both sides by 21} \\ (21x)/(21)=(14)/(21) \\ x=(14)/(21)=(2)/(3) \end{gathered}`

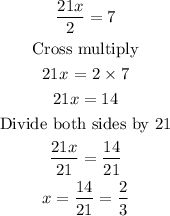
(d) Find the value of x that makes f(x) = h(x)

f(x) = 9x - 2

h(x) = 4x - 7/4

When f(x) = h(x)

9x - 2 = 4x - (7/4)

9x - 4x = 2 - (7/4)

5x = (1/4)

`\begin{gathered} 5x=(1)/(4) \\ \text{Divide both sides by 5} \\ (5x)/(5)=(1)/(4*5) \\ x\text{ =}(1)/(20) \end{gathered}`

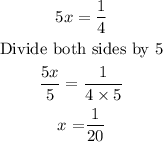
(e) Find the x-intercept of h(x).

h(x) = 4x - 7/4

The x-intercept is the value of x when h(x) = 0

When h(x) = 0

4x - (7/4) = 0

4x = (7/4)

`\begin{gathered} 4x=(7)/(4) \\ \text{Divide both sides by 4} \\ (4x)/(4)=(7)/(4*4) \\ x=(7)/(16) \end{gathered}`

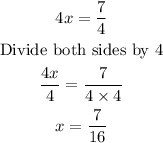
Hope this Helps!!!