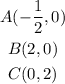Question

In this figure, the curve y= 3x+2-2x^2 cuts the x-axis at two points A and B, and the y-axis at the point C. Find the coordinates of A, B and C

Answer 1

To find the x-coordinates of A and B, find the zeroes of the equation (set y=0 and solve for x).

`y=3x+2-2x^2`

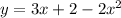
If y=0 then:

`0=3x+2-2x^2`

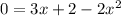
Writing this quadratic equation in standard form, we get:

`2x^2-3x-2=0`

Use the quadratic formula to find the solutions for x:

`\begin{gathered} \Rightarrow x=\frac{-(-3)\pm\sqrt[]{(-3)^2-4(2)(-2)}}{2(2)} \\ =\frac{3\pm\sqrt[]{9+16}}{4} \\ =\frac{3\pm\sqrt[]{25}}{4} \\ =(3\pm5)/(4) \\ \Rightarrow x_1=(3+5)/(4)=(8)/(4)=2 \\ \Rightarrow x_2=(3-5)/(4)=(-2)/(4)=-(1)/(2) \end{gathered}`

Then, the x-coordinate of A is -1/2, and the x-coordinate of B is 2. Both the y-coordinate of A and B are 0.

On the other hand, to find the y-coordinate of C, which is the point where the graph crosses the Y-axis, replace x=0:

`\begin{gathered} y=3(0)+2-2(0)^2 \\ =2 \end{gathered}`

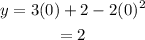
Therefore, the coordinates of A, B and C are:

`\begin{gathered} A(-(1)/(2),0) \\ B(2,0) \\ C(0,2) \end{gathered}`