The equation of the conic section is:
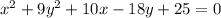
Square terms are positive and have different coefficients. Then, we can say it is an ellipse.
To find the vertex form, we need to group x and y:
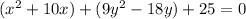
The grouped terms of y can be factored:
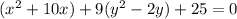
It will be convenient to group the 25 with the group of x, since we can have a perfect square trinomial (since the square root of 25 is 5, which is half ten):
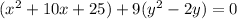
We can factor the first goup:
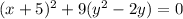
Now, we can try to make another perfect square trinomila from the second term. We need a number whose square root multiplied by 2 gives us 2 (the coefficient of y) This number will be one. Then, we can sum 1 inside the parenthesis, but we need to substract 9 outside it in order not to alter the equation. (it is 9 because we added 1 inside a parenthesis that is multiplied by 9).

Now, we can factor the second group of terms and reorganize:
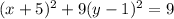
Now, to get the equation in the vertex form, we need a 1 in the right side of the equation. Then, we can divide everything (both sides) by 9:
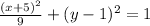
The equation of the ellipse is now on its vertex form. Since the number dividing the x term (9) is higher than the number dividing the y term (1) we can say that the direction of the ellipse is horizontal. It´s longer axis is parallel to the x axis of the plane.