ANSWER
Vertex = (-6, 0) Option B
Graph:
Step-by-step explanation
Given:
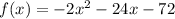
Desired Outcome:
Vertex and graph
Rewrite the equation in vertex form

where:
(h, k) is the vertex.
Now, determine the vertex of the equation
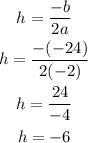
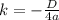
Let's determine the value of D
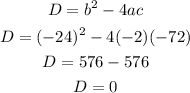
Now,
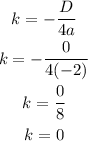
Therefore, the vertex (h, k) = (-6, 0) and when we plot this on a graph, we have:
Hence, the correct option is B.