The rate of change of a function is the increase or decrease that a function experiences as the independent variable changes from one value to another.
The corresponding equation of the average rate of change is:
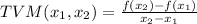
In this case, x1 is 3 and x2 is 3
Remember that according to the notation of the limits, they take the values of 2 and 3.
Now, we solve f(3) and f(2)
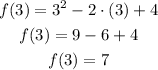

This way now we can replace the values in the TVM equation and I will solve this.
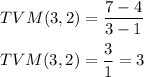
In conclusion, the average rate of change of the function