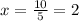Question

3. By elimination 2x - 3y =- 55x + 2y =16

Answer 1

By elimination, it means that we should apply algebraic operations so we find the value of one variable. So first, lets multiply the first equation by 5. We get

`5\cdot(2x-3y)=5\cdot-5\text{ = 10x-15y = -25}`

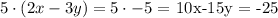
Now, lets multiply by 2 the second equation

`2\cdot(5x+2y)\text{ = 16}\cdot2\text{ = 10x+4y=32}`

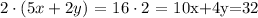
With this two equations, lets subtract the second equation from the first equation

`10x+4y-(10x-15y)\text{ = 32-(-25)}`

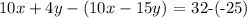
We get

`19y\text{ = 57}`

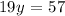
If we divide y by 19 we get

`y=(57)/(19)=3`

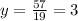
Now, using this value in the second equation we get

`5x+2\cdot3\text{ = 16 }=5x+6`

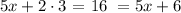
If we subtract 6 on both sides, we get

`16-6\text{ = 5x = 10}`

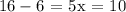
Finally, we divide by 5 on both sides and we get

`x=(10)/(5)=2`