The probability of an event is determined a follows;
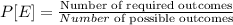
We shall begin with the probability of selecting an even number as shown below;
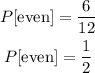
Next we shall calculate the probability of selecting a number less than 5 as shown below;
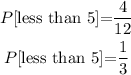
The probability of event A OR event B occuring is calculated a follows;

The probability of selecting an even number or a number less than 5 is therefore

The correct answer is option A