Question

Rachel is bowling with her friends. Her bowling ball has a radius of 4.1 inches. As she bowls she tracks the location of the finger hole above the ground. She starts tracking the location when the finger hole is at the 12 o'clock position and she notices that she got some backspin on the ball and it rotates counter-clockwise.Write a function f that determines the height of the finger hole above the ground (in inches) in terms of the number of radians a the ball has rotated since she started tracking the finger hole. (Note that aa is a number of radians swept out from the 12-o'clock position.)f(a)=

Answer 1

Given that radius is r= 4.1 inches.

let track the location of finger hole is at 12 o'clock.

i.e. the angle is 0 degree.

at 12 o'clock

`\theta=0`

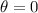
Now when the finger hole changed by 45 degree:

`\theta=45`

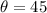
Now convert 45 degree into radians:

`\begin{gathered} \theta=45*(\pi)/(180) \\ \theta=(\pi)/(4) \end{gathered}`

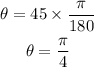
So angle is such that:

`\begin{gathered} \theta\in\lbrack0,(\pi)/(4)\rbrack \\ 0\leq\theta\leq(\pi)/(4) \end{gathered}`

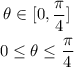
Now calculate the measure of function in polar coordinates:

`\begin{gathered} \theta=0,\text{ f(}\theta\text{)}=r \\ \theta=(\pi)/(2),\text{ f(}\theta)=r\cos \theta \end{gathered}`

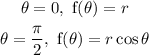
Taking measurement of function:

`\begin{gathered} f(\theta)=r+r\cos \theta \\ f(\theta)=r(1+\cos \theta) \end{gathered}`

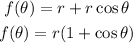
So the function become and the limit is:

`f(\theta)=r(1+\cos \theta),\text{ 0}\leq\theta\leq(\pi)/(4)`