Question

Find the value of x. Round to the nearest tenth.

Answer 1

21.7

Explanation:

Haha, I've done this recently! We are trying to find the hypotenuse, and we know the adjacent side.
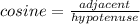`cosine = (adjacent)/(hypotenuse)`, so we can use cosine to help us figure that out. cosine 37° =
`(17.3)/(x)`

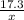
On our calculator, we can determine that cosine of 37 degrees is 0.79863551004, and therefore 0.79863551004 = 17.3/x. Multiplying both sides by x gives 0.79863551004x = 17.3. Finally, all we have to do is divide 17.3 by 0.79863551004 and we get 21.661, rounded to the nearest tenth, 21.7!

I hope this helps!

Answer 2

Given :-

• A right angled triangle is given to us .

To Find :-

• The value of x.

Solution :-

In the given triangle one of the angle is 37° and one of its side is 17.3 . As we know that in a right angled triangle ,

`\longrightarrow cos\theta =(base)/(hypotenuse)`

Substitute ,

`\longrightarrow cos37^o =(17.3)/(x)`

• Value of cos37° is 4/5 .

`\longrightarrow (4)/(5)=(17.3)/(x)`

Cross multiply ,

`\longrightarrow x =(17.3* 5)/(4)`

Simplify ,

`\longrightarrow \underline{\underline{x = 21.625}}`

Hence the value of x is 21.625.